Quantum state tomography
To understand the physical process in a quantum information
processing train, and to implement quantum communication schemes
without an explicit reference frame it is often necessary to carry out
a complete determination of the quantum state of a qubit or a set of
qubits.
There have been several implementations of quantum state tomography
for photonic qubits and multiqubit states; in this project, we
implement a minimal and optimal scheme for this purpose, based on a
POVM scheme which recently caught attention both in the quantum
information community [1] and for polarization
measurements in classical optics [2].
The scheme relies on a four-valued measurement outcome for a single
photon entering the analyzer, with each of the measurement outcomes
corresponding to a polarization or qubit state maximally separated from
the states corresponding to the other three detectors; these four
states can be represented as a tetrahedron in the Poincare sphere
representing the polarisation state of a single photon, or a classical
light field:
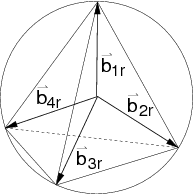
We have three short movies illustrating how such a scheme can be used to determine an unknown polarization state. We use a cylindrical projection of a Poincare sphere, so that we have a "map" of the surface of the sphere. We then prepare three distinct maximally pure polarization states, and accumulate photon numbers at each detector. With each marginal photon, a distribution is built up, and the polarization state can be estimated from this distribution. We accumulate a total of 150 photons. In the movies, the prepared state is marked by a white cross, while the estimated state is marked by a red cross. We have also illustrated a region of arbitrary high likelihood - this region is marked by white. The green line marks the "equator" corresponding to linear polarization states.
- The first movie is for horizontally polarized light.
- The second movie is for a state that is aligned to one of the tetrahedron directions.
- The third movie is for a state that is anti-aligned to the previous direction.
We implemented such a measurement scheme using an arrangement of
partially polarizing beamsplitters and single photon detectors in a
robust experimental setup, allowing us to determine the polarization
state both for pure states (or polarized light in classical optics) and
mixed states (corresponding to partially polarized light) [3]:
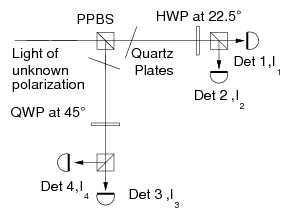
With such a scheme, optimal state tomography can be carried out both
for single photon states and multiphoton states [4], allowing to
quickly estimate the polarization change e.g. in an optical fiber used
for quantum key disribution.
Such a measurement scheme is also useful for an implementatin of a
new quantum key distribution protocol, based exactly on correlations
between tetrahedral POVMs on both twins of a photon pair in a entangled
singlet state [5].
References:
| [1] | Rehacek, B.-G. Englert, and D. Kaszlikowski, Phys. Rev. A 70, 052321 (2004) |
| [2] | R.M.A. Azzam and F.S. Sudrajat, Appl. Opt. 44, 190-196 (2005) |
| [3] | A. Ling et al., J. Mod. Opt. 53, 1523 (2006) |
| [4] | A. Ling et al., PRA 74, 022309 (2006) |
| [5] | B.-G. Englert, D. Kaszlikowski, H.K. Ng, W.K. Chua, J. Rehacek, and J. Anders, quant-ph/04120752005) |

