Exploring the Limits of Non-Locality with Pairs of Photons

Bell inequalities are a powerful tool in discriminating whether Nature is better described by classical theories or non-local ones. We experimentally test Bell inequalities and the predictions of standard quantum mechanics using a source of polarization entangled photon pairs. Two such tests that we performed include an attempt to saturate the Tsirelson bound, the well known 2√2 predicted by standard quantum mechanics, which allowed us to exclude some of the alternative, non-local theories [1]. We also tested a different approach to discriminate between classical and non-classical system based on the computational complexity of the output, as opposed to the statistical nature of the standard Bell tests [2].

Experimental Setup

For these two experiments, we built a typical polarization-entangled photon pair source in a crossed-ring configuration at 810 nm. Careful balancing of the |HV> and |VH> contribution and adjustment of their relative phase using the compensation crystals (CC) yield a very clean singlet state |ψ^- >. We minimize contributions from higher order parametric conversion processes by restricting the pump power to 7 mW.

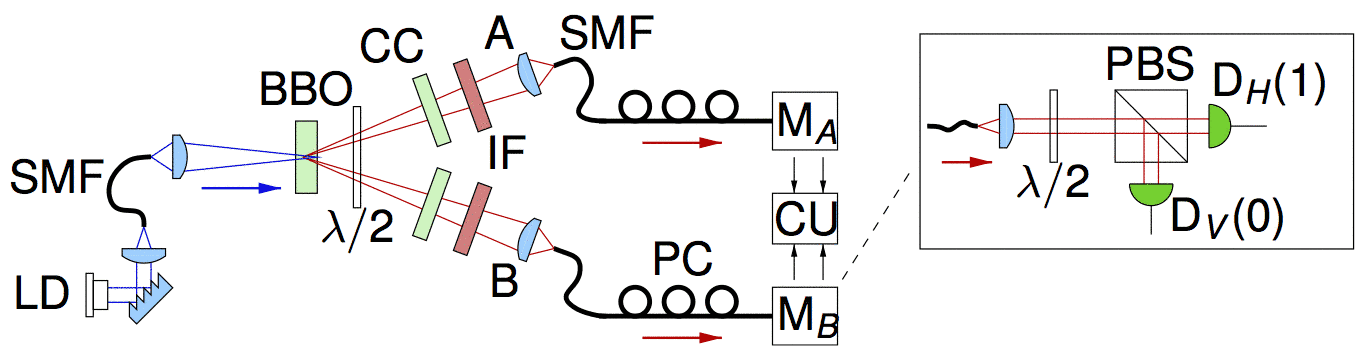
We observed both in the natural H/V and complementary ±45° basis, high visibility of V = 99.9±0.1%, indicating a high quality of polarization entanglement. In the first experiment, polarization analysis is being perform using film polarizers (extinction ration 10^-5) in front of the collection optics. This eliminates any unwanted polarization state transformations due to fiber neutralization. In the second experiment,polarization is projected by λ/2 plates and polarization beam splitter in each analyzer after the single mode fibre (see inset). Photons are detected by APDs, and corresponding detection events from the same pair identified as a coincidence if they arrive within ±1.2 ns of each other.

Approaching Tsierlson Bound

According to quantum theory, |S| has an upper bound of 2√2 ≈ 2.82843 (Tsirelson bound). Other non-local theories predict different upper bounds. For example, a model proposed by Grinbaum [5] predicts a bound of 2.82537(2) (Grinbaum bound), slightly smaller than the Tsirelson bound, but also consistent with all the available experimental results obtained so far. The underlying theory tries to address the cut between the observer and the observed system in quantum mechanics, supporting the hypothesis that quantum theory is only an effective description of a more fundamental theory.

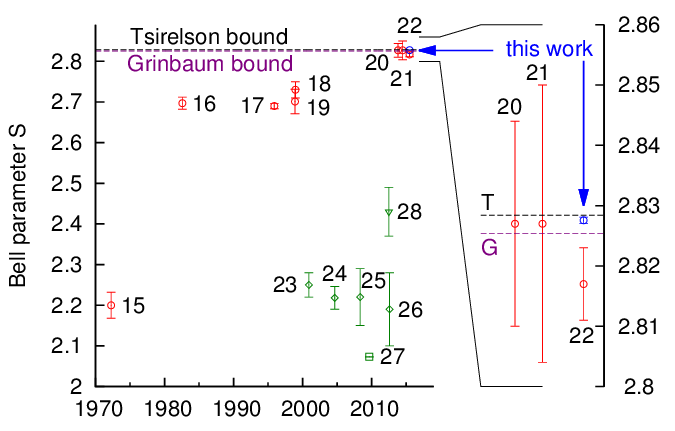
In this experiment, we collected for 312 times a complete set of 16 measurements needed to evaluate the S parameter, for a total of 33,184,329 pair events. We obtained a final a value of S = 2.82759±0.00051, or a separation of 2√2 - S = 0.00084±0.00051 from the Tsirelson bound. This value violates Grinbaum bound, thus refuting his theory.

Quantum Test Based on Compression Software

Standard Bell tests are based on statistical inference of correlations between measurements. We adopt an algorithmic approach and replace correlation with a distance based on Kolmogorov complexity [6].

We estimate the Kolmogorov complexity of a string x by the length of a string after compression with a commercial compression software, C(x). The Normalized Compression Distance (NCD) is a measure of how similar two strings x and y are:

NCD(x, y) = ^{C(x, y) - min{C(x), C(y)}}⁄_{max{C(x), C(y)}}

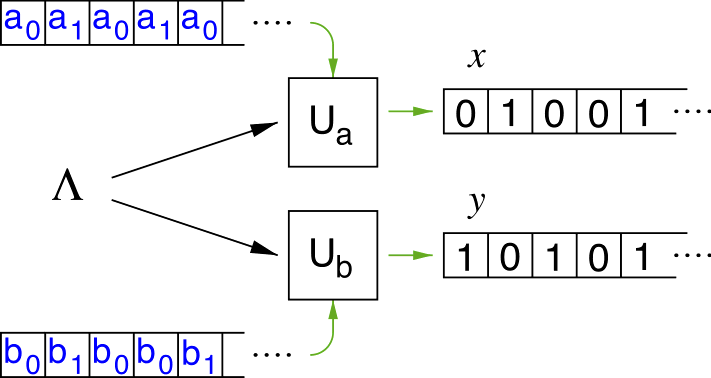
A local hidden variable theory that describes the outputs two machines can be encoded in a common input program, and additional programs for each UTM encoding the sequence of local measurement settings a_j and b_k (j, k = 0, 1). An experimental result that cannot be simulated by the UTMs would therefore falsify any local realistic description of that process.

We define an algorithmic Bell inequality given by:

S_A = NCD(x₀, y₁) - NCD(x₀, y₀) - NCD(x₁, y₀) - NCD(x₁, y₀) ≤ 0

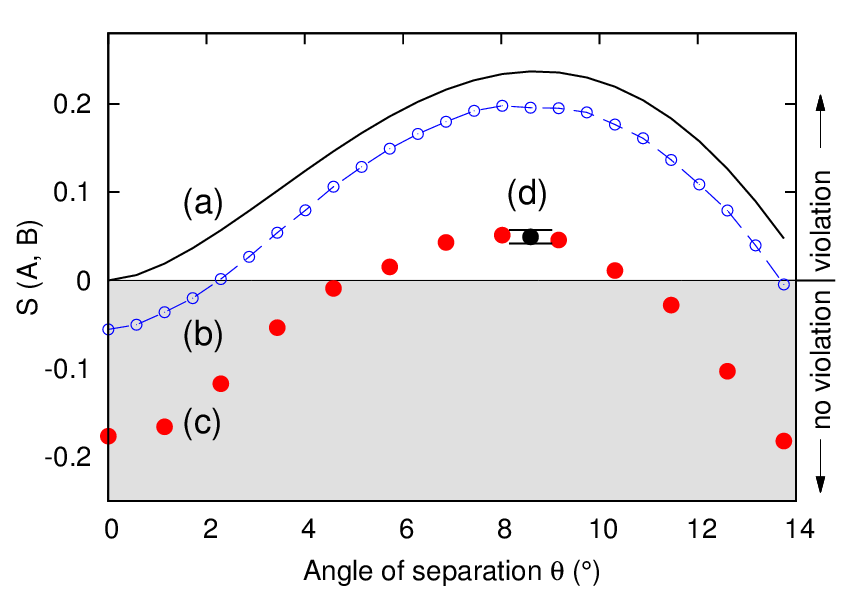
If S_A is positive the local realism hypothesis is violated. We experimentally tested inequality (2) using the setup of figure 1, choosing set of polarization projection a ⃗ ₀ . b ⃗ ₁ = cos 3θ and a ⃗ ₀ . b ⃗ ₀ = a ⃗ ₁ . b ⃗ ₀ = a ⃗ ₁ . b ⃗ ₁ = cos θ, for a range of the angle θ.

To estimate an uncertainty of the experimentally obtained values for S_A, we set θ = 8.6°, for which we expect the maximum violation, and collected results from a larger number of photon pairs. We repeated the measurement of S 8 times, and considered the average value and standard deviation of this set obtaining the final result of S(θ = 8.6°) = 0.0494±0.0076.

References

[1]	H. S. Poh, S. K. Joshi, A. Cerè, A. Cabello, and, C. Kurtsiefer, Approaching Tsirelson's Bound in a Photon Pair Experiment , Phys. Rev. Lett. 115, 180408 (2015).
[2]	H. S. Poh, M. Markiewicz, P. Kurzynski, A. Cerè, D. Kaszlikowski, and, C. Kurtsiefer, Probing Quantum-Classical Boundary with Compression Software, New J. Phys. 18, 035011 (2016).
[3]	J.F. Clauser, M.A. Horne, A. Shimony, R.A. Holt, Phys. Rev. A 23, 880 (1969).
[4]	B. Cirelson, Lett. Math. Phys. 4, 93 (1980).
[5]	A. Grinbaum, Found. Phys. 45,1341-1350 (2015).