Magnetometry with single NV centers in diamond
Magnetometers based on quantum systems promise high sensitivities but are often not practical for real-world applications as they usually require either cryogenic temperatures or complex laser systems. An exception is the electron spin of the NV center in diamond. These defects in the diamond lattice behave like single atoms trapped in the crystal and their unique internal dynamics allows one to perform optical spin polarization and read-out. The magnetic field at the NV center is measured simply by finding the spin flip frequency. Like for free electrons the electron spin resonance of the NV center depends linearly on the magnetic field, thanks to the Zeeman-effect. One strong point of the NV centers is that the experimental setup can be potentially miniaturized to a volume of a few cm3.
Experimental Setup
We employ synthetic diamonds (nitrogen concentration: <5 ppb) in which individual NV centers are separated by several micrometers. The low concentration of NV centers allows us to optically address single centers using a home-built confocal microscope (Figure 1a). We excite the NV centers with laser light at a wavelength of 532 nm and detect the red-shifted fluorescence (630-750nm) with a single photon detector. The photon detection rate for a single NV center is 5x104 counts per second with a signal-to-background ratio of 50.
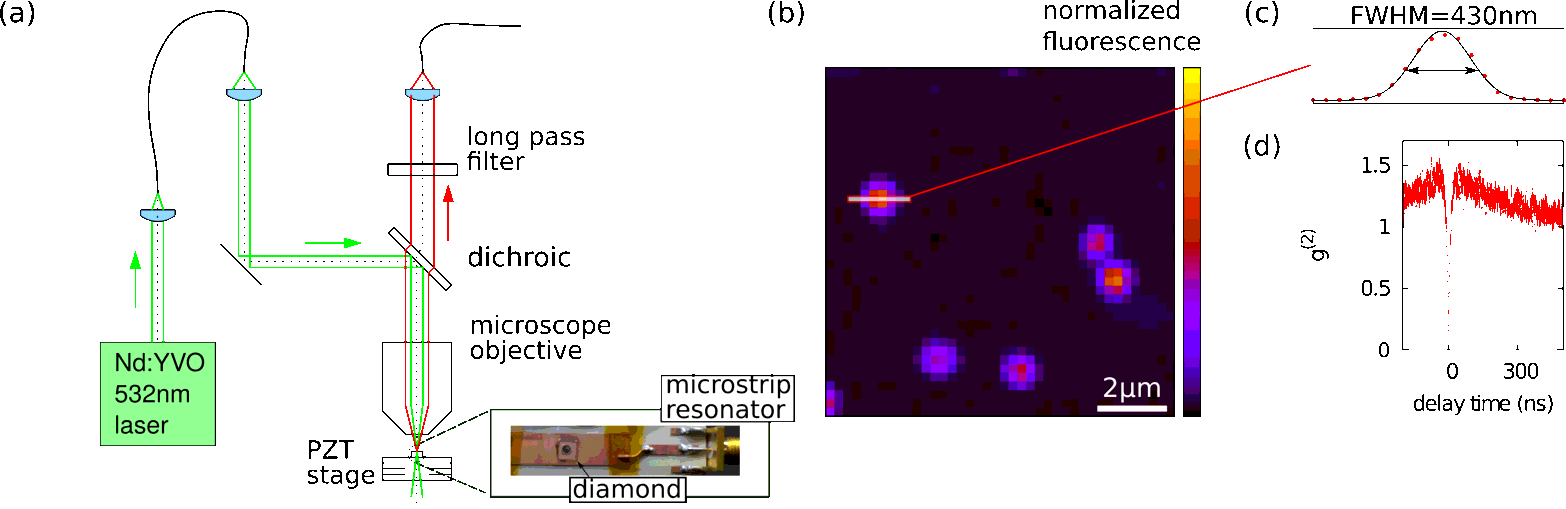
Figure 1b shows the detected fluorescence for a scan of the diamond position; several NV centers are clearly resolved. We verify that we address single centers by measuring the second-order correlation function of the emitted fluorescence with a Hanbury-Brown and Twiss setup (Figure 1d).
Optically detected magnetic resonance (ODMR)
The ground-state of the NV center is an electron spin-1 system with large zero-field splitting which separates the |0> (|mf>) state from the |±1> states by 2.87 GHz (Figure 2a). Thus, the |±1> are energetically degenerate. Any external magnetic field lifts this degeneracy and measurements of the resulting energy shifts are used to determine the magnetic field strength. With a shift of 2.8 MHz per Gauss the energy levels are very sensitive to fields along the symmetry axis of the NV center. The energy differences between the spin states are measured by optically detected magnetic resonance (ODMR).
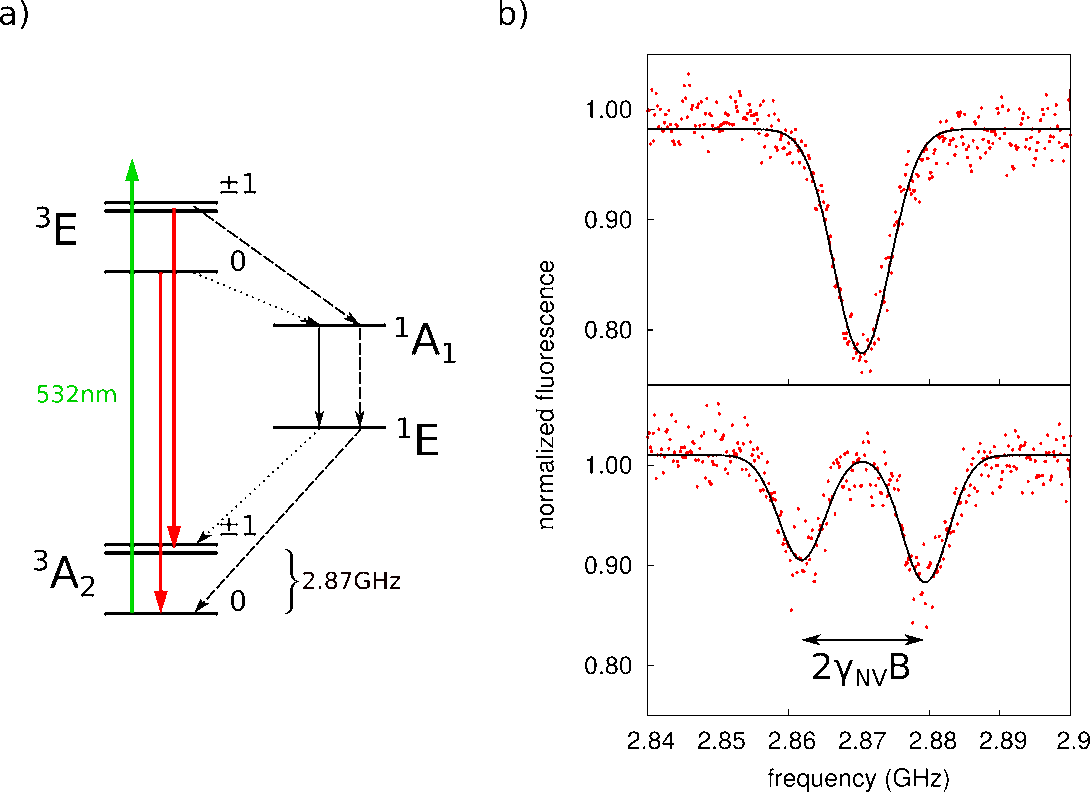
The particularities of the energy level structure of the NV center allows one to optically prepare and read out the electron spin and even make single spin detection possible (Figure 2b). There are two main effects; first, under continuous excitation with 532 nm light the electron spin is pumped into the |0> state. This spin pumping is very effective and leads to a high spin polarization (>90%) within a few hundred nanoseconds even at room temperature. Secondly, the emitted fluorescence depends on the spin state and is 30% higher for |0> ('bright') state than for the |±1> ('dark') states. Therefore the spin state can be determined from the detected fluorescence.
The electron spin is rotated by applying an oscillating magnetic field resonant with a magnetic dipole allowed transition (Δmf=|1|). To this end, we place the diamond on a home-built microstrip resonator which is resonant at 2.87 GHz with a quality factor of 30. The microwave is generated by a digital synthesizer and capacitively fed into the resonator with a coupling efficiency of 95%. The use of a resonator greatly reduces the requirements for the microwave amplifier. Under continuous laser excitation electron spin flips are observed as transitions from the 'bright' to the 'dark' state and therefore as reduction of the detected fluorescence while scanning the microwave frequency (Figure 2b).
We apply an external magnetic field along the NV axis which lifts the degeneracy of the |±1> states and observe the Zeeman splitting (Figure 2c). The obtained spectrum can be used to determine the magnetic field strength, however, the magnetic field sensitivity is limited by the power broadened linewidth of the transition. A much better sensitivity is achieved by using coherent spin rotations which eliminate the power-broadening from the spectrum while keeping a high signal-to-noise ratio.
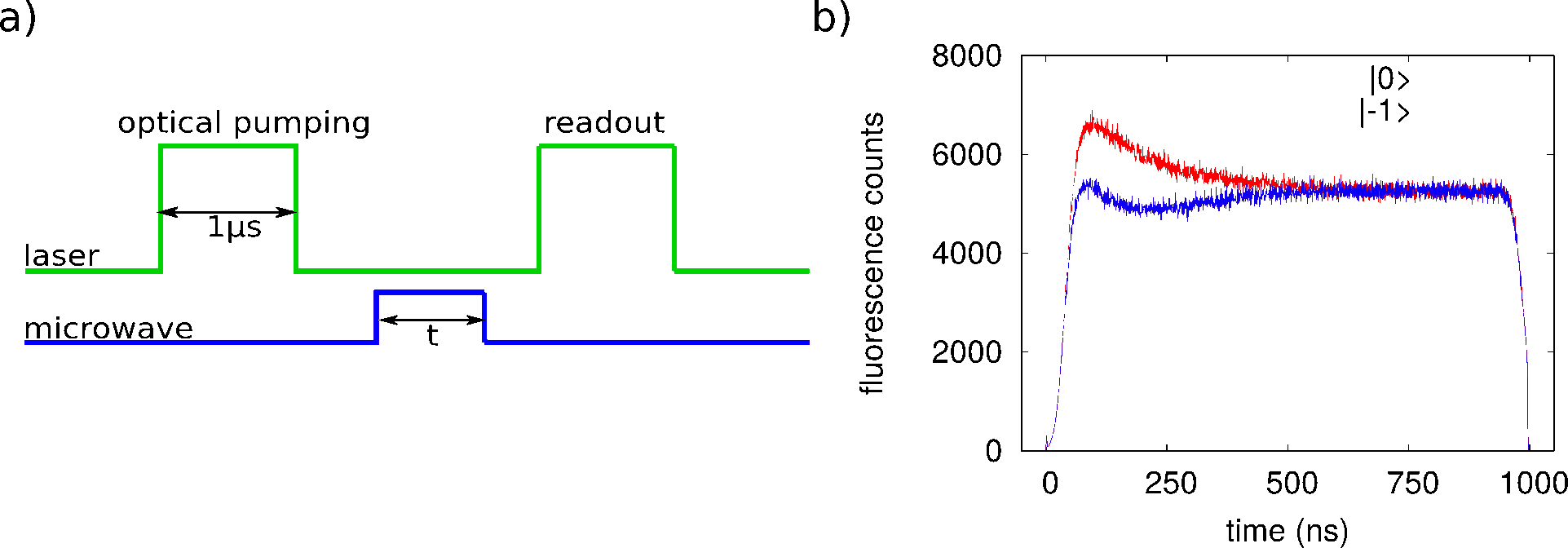
For coherent spin manipulation we divide the measurement cycle into three parts: preparation, manipulation and read-out. The preparation phase consists of a 1 μs-long laser pulse which prepares the NV in the |0> state. Subsequently a microwave pulse is applied for a certain duration and finally a second laser pulse is used to read out the spin state. We determine the spin state from the fluorescence during the first 300 ns of the read-out pulse.
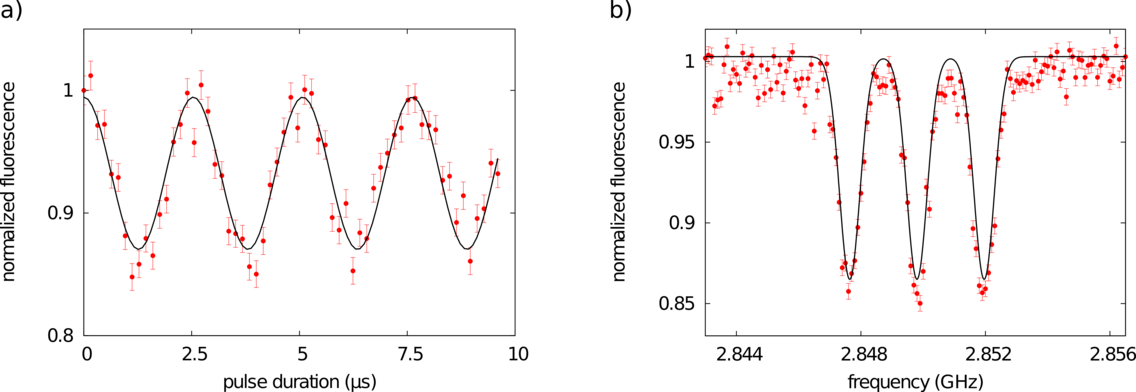
The normalized fluorescence for different durations of the microwave pulse in Figure 3a shows an example of a coherent spin nutation between the |0> and the |-1> state. We obtain an ODMR spectrum without any power broadening but with the best signal-to-noise ratio (Figure 3b) by choosing an appropriate duration of the microwave pulse to invert the spin state (π-pulse).
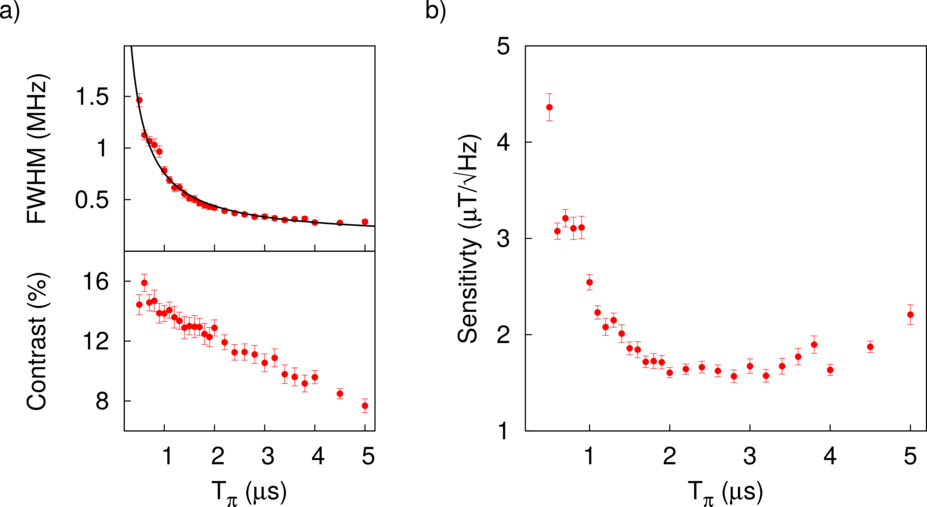
In order to find the optimal magnetic sensitivity we study the linewidth and contrast of the electron spin transition for different microwave powers corresponding to different lengths of the π-pulse (Figure 4a). For short π-pulses the linewidth is dominated by the spectral width of the pulse and therefore the linewidth decreases with increasing π-time until it reaches the limit given by the electron spin coherence time. For our diamond sample the linewidth (FWHM) settles at 200 kHz which corresponds to a coherence time T2*= 2-3 μs. Taking the linewidth and the contrast measurements into account we calculate the magnetic field sensitivity and find a sensitivity of 1.6 mT/√Hz when the π-time equals the coherence time T2* (Figure 4b).
There are several ways to improve the sensitivity, for example, by measuring many NV centres simultaneously or collecting more of the NV fluorescence. Pushing NV-technology towards a magnetometer which is robust, handy and more sensitive than existing technologies is an exciting challenge.
References
| [1] | L Rondin et al, Rep. Prog. Phys. 77 056503 (2014) |

