Thermal Light and Applications

Light from thermal black body radiators such as stars exhibits photon bunching behavior at sufficiently short time-scales [1]. However, with available detector bandwidths, the characteristic bunching signal in the second order correlation function g⁽²⁾ is difficult observe directly.

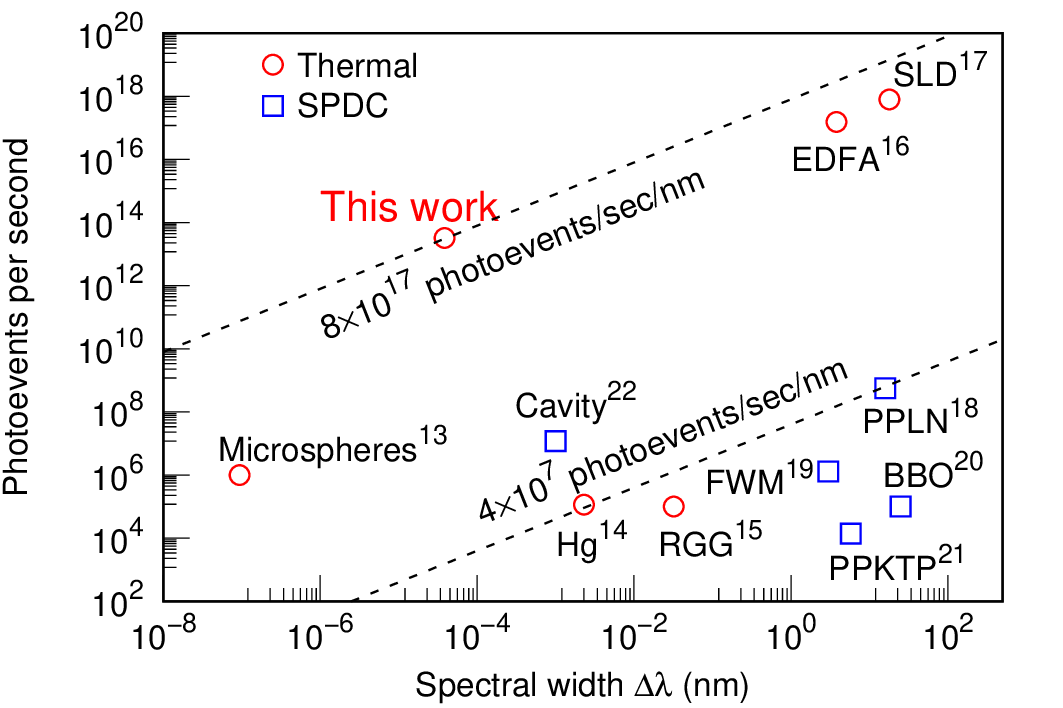
We work on experimental techniques to increase the photon bunching signal from various thermal light sources, including blackbody radiation via spectral filtering of the light source. Our measurements reveal strong temporal photon bunching from blackbody radiation, including the Sun [2].

Beyond reviving the interest in intensity interferometry as a tool in astronomy first demonstrated by Hanbury-Brown and Twiss [3], we explore how thermal light can be used in a number of modern sensing applications.

Revealing Thermal Nature of Blackbody Light Sources

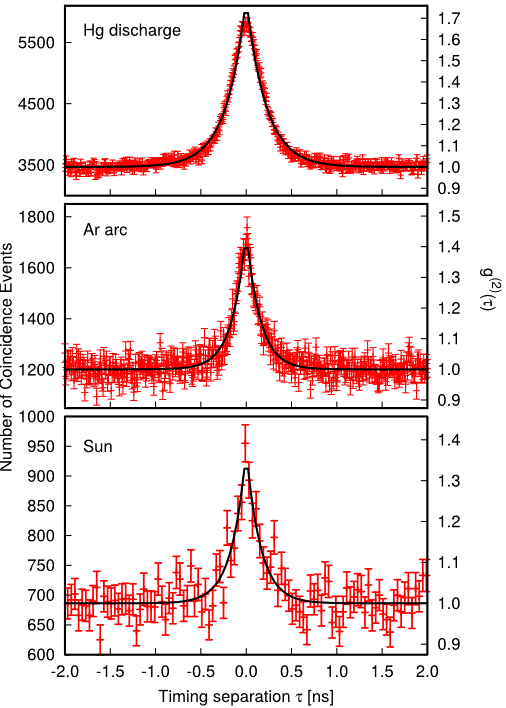
The coherence time scale of thermal photon bunching is approximately inversely proportional to the spectral width of the associated light source. For a discrete spectral line of a gas discharge lamp, the coherence time of its photon bunching behavior is easily measurable. For blackbody sources like the Sun or an Arc lamp, however, coherence times around 5 fs make it difficult to directly observe the thermal photon bunching signature in the second order correlation function g⁽²⁾(τ).

The coherence time of the light source can be increased via a two-step spectral filtering with a grating and an etalon before recording two-photon temporal correlations with two Avalanche photodetectors in a Hanburry-Brown--Twiss configuration:

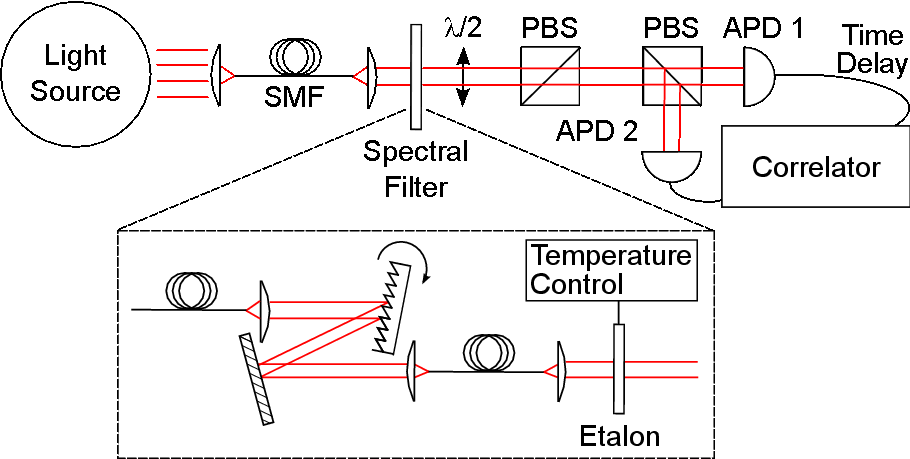
Various light sources are investigated with this filtering scheme, all revealing their thermal photon statistics with a very strong signal-to-noise ratio:

Read the papers:
P.K. Tan, G.H. Yeo, H.S. Poh, A.H. Chan, C. Kurtsiefer, Astrophysics Journal Letters 789, L10 (2014);
P.K. Tan and C. Kurtsiefer, MNRAS 469, 1617-1621 (2017).

Range Sensing with Thermal Light

Conventional optical ranging (lidar) require time-modulated light sources to carry out a time-of-flight measurements [5], opening up vulnerabilities to spoofing attacks as well as being non-stealth.

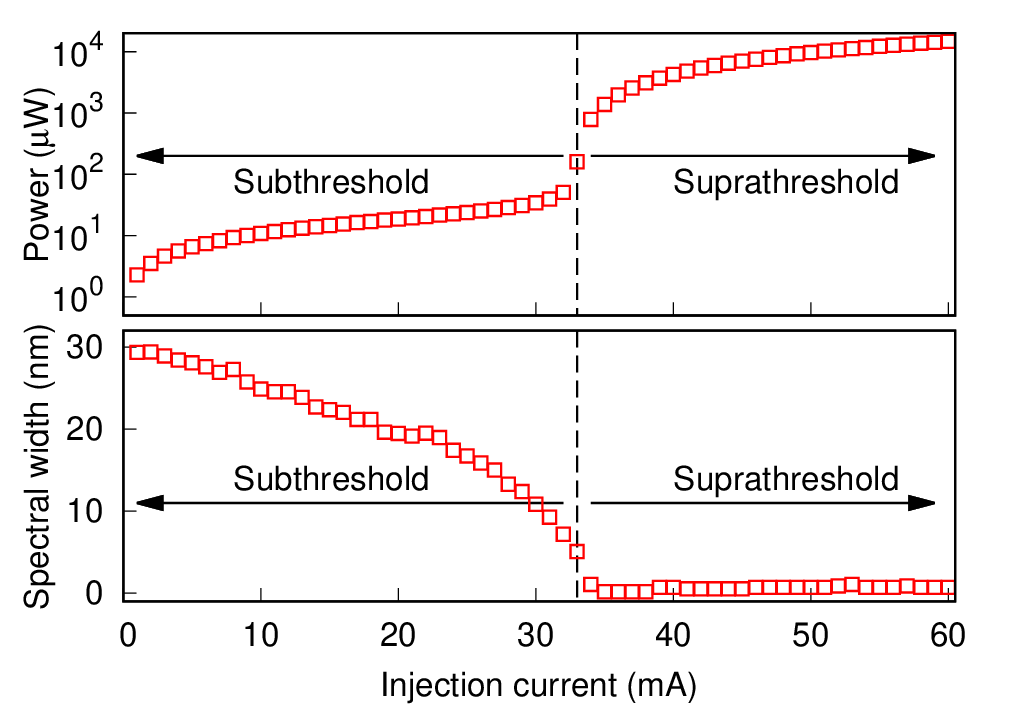
We use a subthreshold laser diode exhibiting as a stationary source with thermal photon bunching, providing an unprecedented brightness for using thermal light for range sensing:

In our experiment, thermal light from a subthreshold laser diode (LD) is split (BS) into a reference beam, and then a probe beam which illuminates the target retroreflector. The beams are spectrally filtered (E, BP1, BP2) before timestamped by a pair of detectors. Time-of-flight measurements are extracted from the g⁽²⁾(τ) peaks in the two-photoevent coincidences:

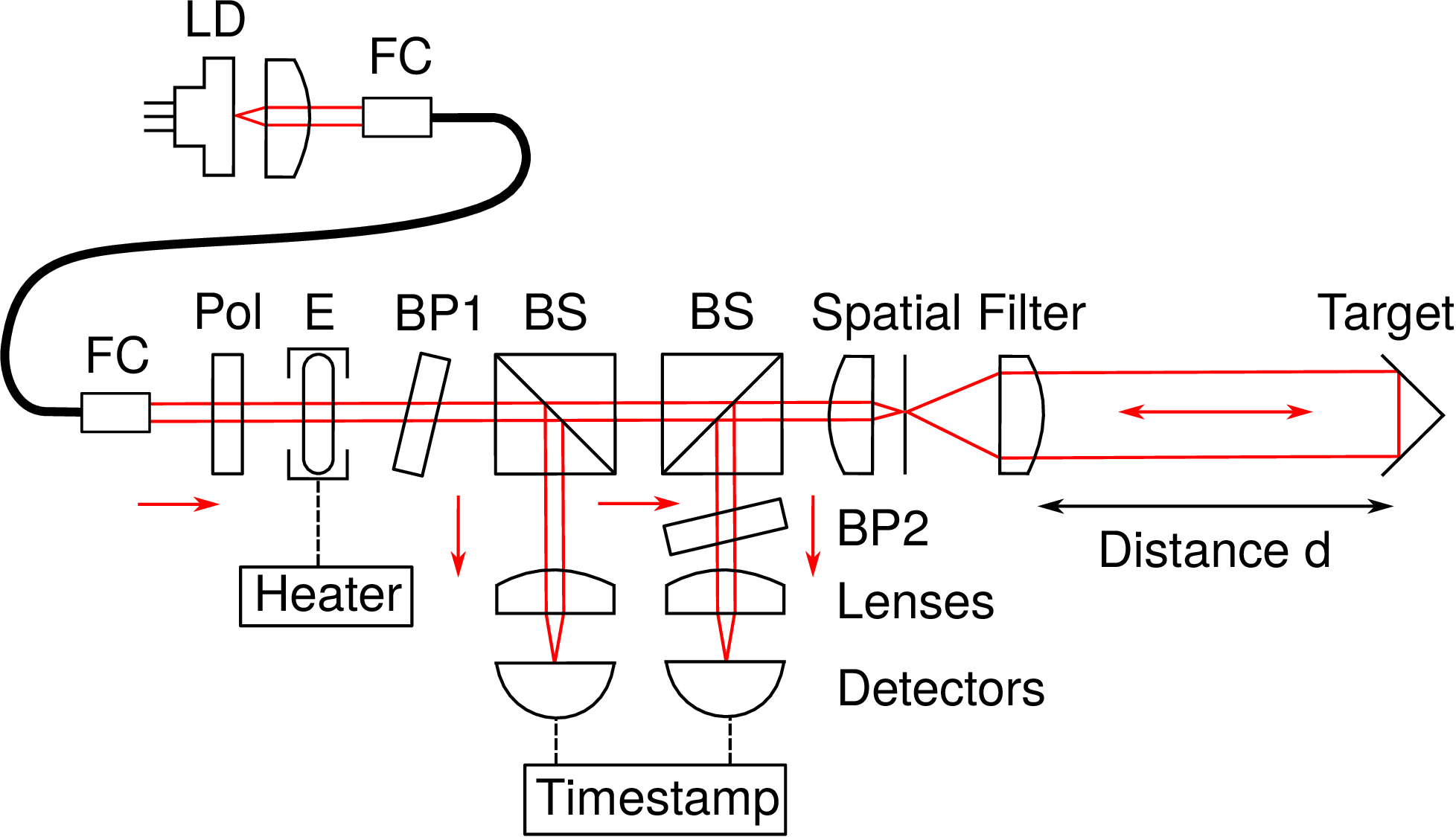
Experimental results exhibit a clearly resolvable thermal signature for distances on a range of a 1..2 km, showcasing the viability of using thermal light as a quantum lidar:

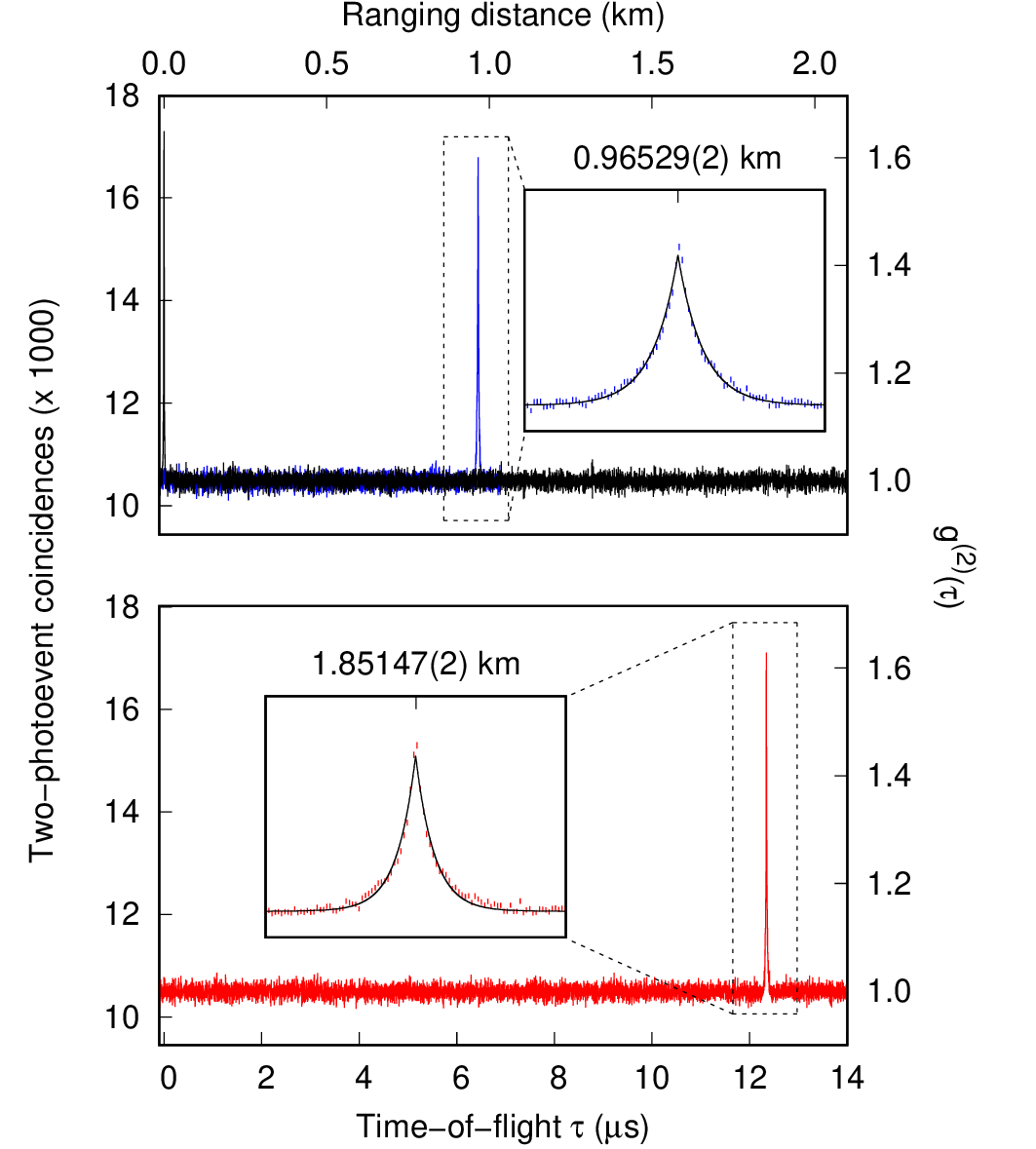
Read the paper:
P.K. Tan, X.J. Yeo, A.Z.W. Leow, L. Shen, C. Kurtsiefer, Phys. Rev. Applied 20, 014060 (2023).

Distinguishing thermal and coherent light

Emission of light from a laser below its lasing threshold can be a very bright source of thermal light [4], before it emits mostly coherent light above threshold. We utilize an interferometric correlation technique to investigate this transition, which better reveals the coherence time and the thermal nature of the light:

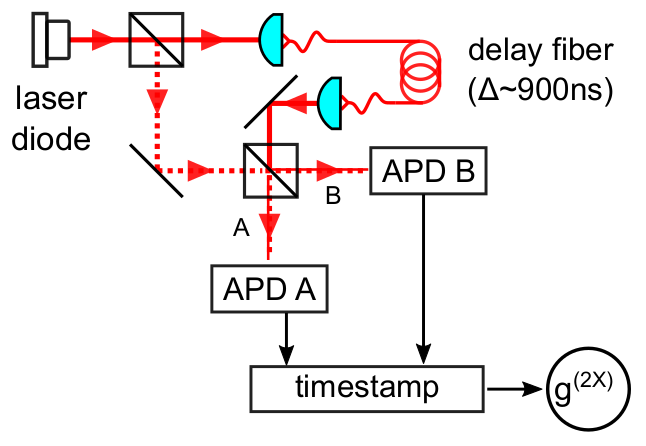
When transiting through the laser threshold, the coherence time τ_c of the emitted light and the fraction ρ of coherent light vs. thermal light can be determined simultaneously:

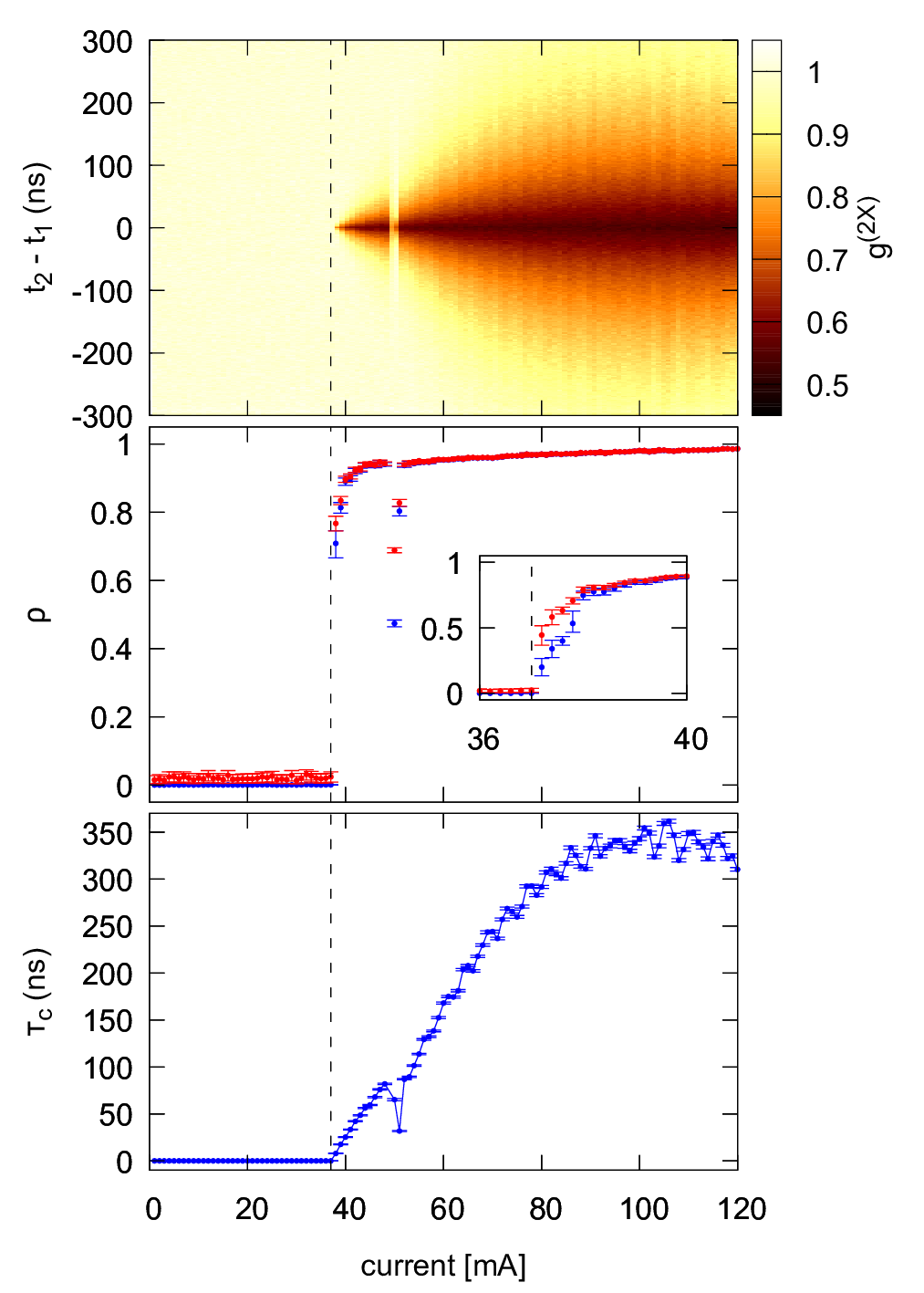
Read the paper:
X.J. Yeo, E. Ernst, A. Leow, J. Hwang, L. Shen, C. Kurtsiefer, P.K. Tan, Phys. Rev. A 109,013706, (2024)

References

[1]	R.J. Glauber, Physical Review 130, 2529 (1963).
[2]	P.K.Tan et.al., Astrophysical Journal Letters, 789, L10 (2014).
[3]	R. Hanbury-Brown & R.Q. Twiss, Nature 178, 1046-1048 (1956).