Single atom-photon quantum interfaces

Atom-photon interfaces will be one of the core building blocks in future quantum information protocols. While photons are ideal carriers for transporting quantum information over long distances, atoms can be used to store and process information.

A very clean implementation of quantum information storage uses the internal degrees of freedom of single, isolated atoms. By localizing a single atom in free space and coupling it to external light fields, we investigate single atom-single photon interactions, which are important for a basic understanding of the underlying physical processes of quantum interfaces.

Cooling and trapping of a single atom

The first step is the preparation of a single atom in a way that a photon can actually interact with it..

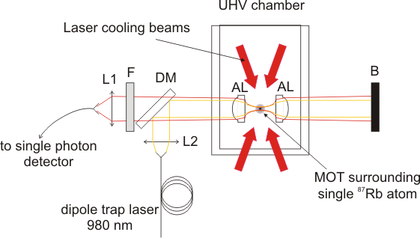We prepare a cloud of cold 87Rubidium atoms using a combination of laser cooling and trapping in a magneto-optical trap (MOT). By overlapping a tightly focused optical dipole trap with the MOT, we can trap a single atom only. Two or more atom trapping events are prevented by the collisional blockage effect [1,2].

Signature of a single atom

A single atom in the trap manifests itself through an anti-bunching effect in the atomic fluorescence: two photons never emerge at the same time.

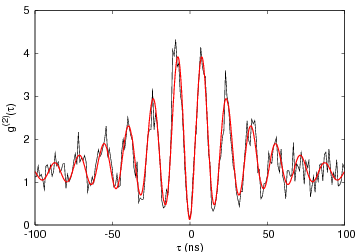We assess this effect by measuring the second order correlation function g(τ), a normalized histogram of time difference between two photodetection events in a Hanbury-Brown-Twiss experiment. Besides the dip in g(τ) at τ=0 which indicates that we only look at a single atom in the trap, we see the Rabi oscillations associated with a coherent evolution of the atom under the influence of near-resonant excitation light.

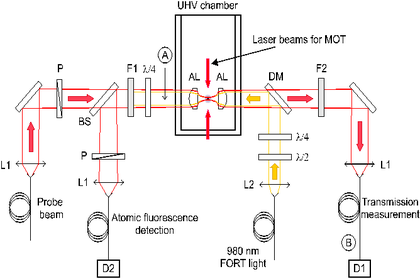
Scattering of light by a single atom

A very common way to have a photon efficiently interacting with a photon involves the field enhancement of the photon mode with the help of optical cavities. In this project, however, we explore an alternative path of strongly focusing the photonic mode. By reaching a light field diameter on the order of the diffraction limit, we should see strong interaction between the photon and the localized atom.
one of the first measurements involved the experimental observation of the extinction (or simply the shadowing) of a light beam focused onto a single atom in our trap. The transmission of a nearly resonant light beam is obtained by comparing the power of the probe beam with and without an atom present in a trap (details in [4]).

The highest scattering probability is expected for coupling a clean two-level system in an atom to resonant probe light. For transitions from the F=2 ⁸⁷Rb ground state driven by circularly polarized light on a D2 line this is the case, and we observe an extinction of 10.4% for one of the circular polarizations. This clearly indicates that the atom can efficiently scatter photons from the light beam even without assistance of cavity.

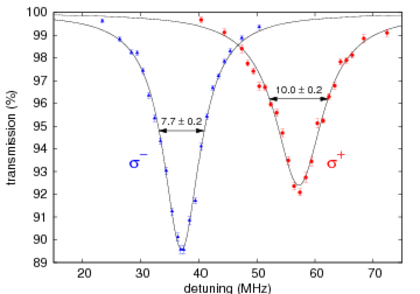
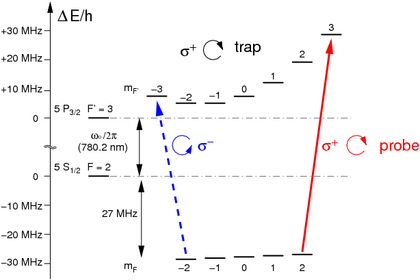
Since we use a circularly polarized optical dipole trap, the atomic energy levels experience an asymmetric AC Stark shift. This effect breaks the degeneracy of the atomic hyperfine levels, and thus the σ⁺ transition appears at a higher frequency than the σ^- transition, and both of them are displaced from the bare atomic resonance frequency. Again, details can be found in [4].

Understanding strong focusing

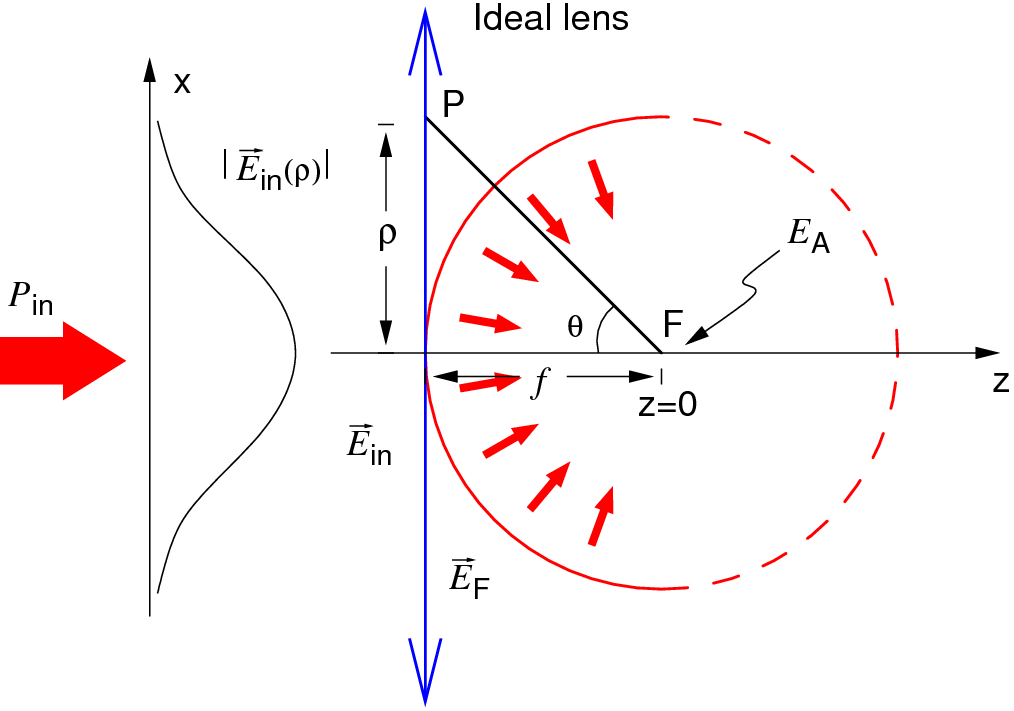
The scattering probability in our experiments can be modeled by the dipolar susceptibility of the single atom, and the focusing properties of a strongly focused Gaussian beam (see left figure). We found analytical expressions for the field at the atom, and evaluated the amount of the light in the original Gaussian mode collected with a second single mode fiber using mode overlap techniques. With this, we find that an extinction of up to 92% should be observable in transmission for a high (but still realistic) numerical aperture of the focusing system (right figure). The focusing strength u refers to the ration of the Gaussian beam waist w before the lens and its focal length f.

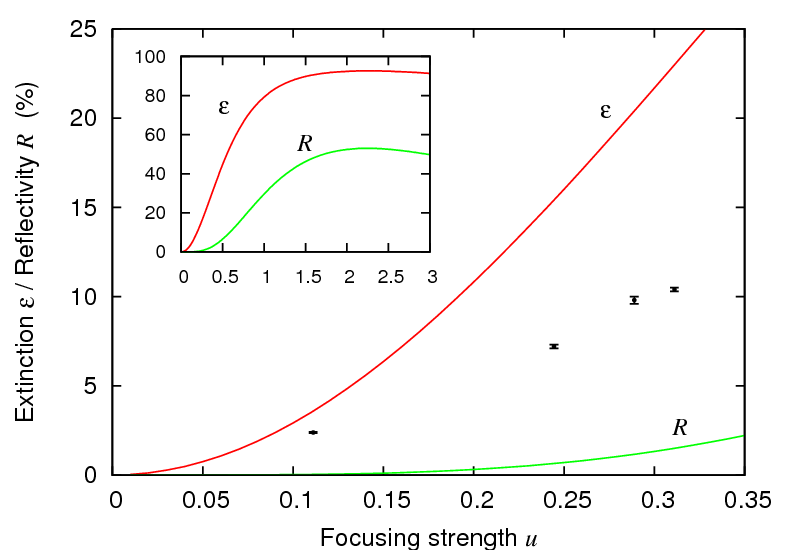We feel that such a result opens a new perspective for quantum information processing with photons and atoms in a free-space configuration. For more details, please refer to [5].

Phase shift measurement

A light beam passing through a dispersive medium (such as a single atom) acquires a phase shift that is related to the absorption /scattering. If the atomic state is altered by one photon, this phase shift can form the basis of a conditional phase gate, one of the missing building blocks to carry out scalable quantum information processing with photonic quits.

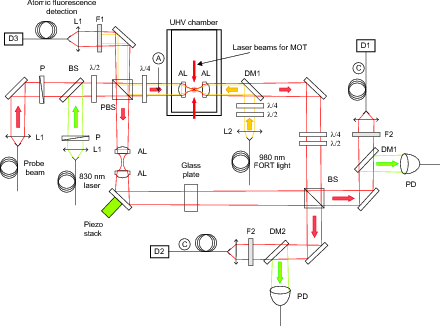
As a first step, we measured the phase a monochromatic, near-resonant light beam beam acquired by the presence of a single atom in one of the hyperfine ground states with a balanced Mach-Zehnder interferometer (left image). The frequency of the probe beam was tuned across the resonance, and we infer the phase shift by measuring the power imbalance at the two output ports of an interferometer.

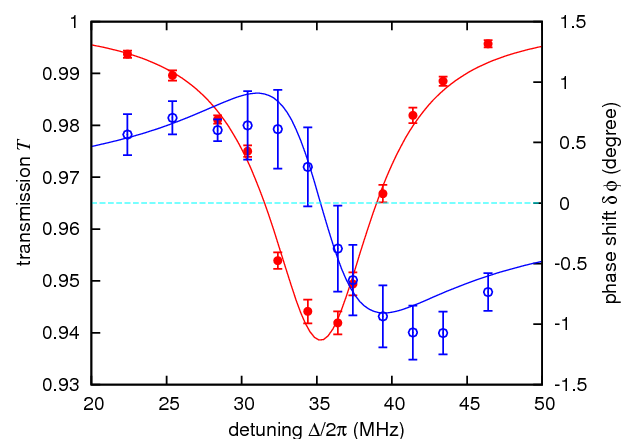So far, we have observed a maximum phase shift of about 1 degree, with room for improvement by increasing the numerical aperture of our focusing system. For more details, please refer to [6].

Pulsed excitation

Transfer of a single excitation of the electromagnetic field (a photon)) to an atom in free space requires not only a matching of the spatial field mode, but also a spectral, or temporal match. In a nice argument brough forward in [8], one can view the absorption process as the temporal inverse of a spontaneous emission, and would expect a resonant light field with a rising exponential temporal envelope as the optimal condition for the absorption of a single photon. We developed techniques to prepare coherent pulses with an exponentially rising envelope [9], and were able to demonstrate that an exponentially rising envelope leads to a higher absorption probability [10].

References

[1]	N. Schlosser, G. Reymond, I.E. Protsenko, and P. Grangier, Nature 411, 1024 (2001)
[2]	N. Schlosser, G. Reymond, P. Grangier, Phys. Rev. Lett. 89, 023005 (2002)
[3]	M. Weber, et al., Phys. Rev. A 73, 043406 (2006)
[4]	M.K. Tey, Z. Chen, S.A. Aljunid, B. Chng, F. Huber, G. Maslennikov and C. Kurtsiefer, Nature Physics 4, 924-927 (2008)
[5]	M.K. Tey, G. Maslennikov, T.C.H. Liew, S.A. Aljunid, F. Huber, B. Chng, Z. Chen, V. Scarani,C. Kurtsiefer, New Journal of Physics 11, 043011 (2009)
[6]	S.A. Aljunid, M.K. Tey, B. Chng, T.C.H Liew, G. Maslennikov, V. Scarani, C. Kurtsiefer, Phys. Rev. Lett. 103, 153601 (2009)
[7]	S.A. Aljunid, B. Chng, M. Paesold, G. Maslennikov, C. Kurtsiefer, J. Mod. Opt. 58, 299-305 (2011)
[8]	M. Sondermann, R. Maiwald, H. Konermann, N. Lindlein, U. Peschel, G. Leuchs, Appl. Phys. B 89, 489 (2007)
[9]	H.L. Dao, S.A. Aljunid, G. Maslennikov, C. Kurtsiefer, Rev. Sci. Instr. 83, 083104 (2012)
[10]	S.A. Aljunid, G. Maslennikov, Y. Wang, H.L. Dao, V. Scarani, C. Kurtsiefer, Phys. Rev. Lett. 111, 103001 (2013)